NotesAtHKU

Newton's laws

Newton's first law

An object will remain at rest or in uniform motion unless acted upon by a force.

Newton's second law

The acceleration of an object is directly proportional to the net force acting on it, and inversely proportional to its mass.

\sum F=ma

Newton's third law

For every action, there is an equal and opposite reaction. This gives rises to forces like friction, normal and tension forces.

Friction

Friction is a force that opposes the motion of an object. It is given by:

F_f=\mu N

Where $\mu$ is the coefficient of friction and $N$ is the normal force experienced by the object.

Conservative force

Conservative forces are forces that do not depend on the path taken by an object. They also have no lost in energy. They include:

Gravitational force
Elastic force
Electric force

Inertia force

Inertia force is the preceived force from the perspective of an accelerating object.

For a person in an elevator accelerating upwards at $a$ , the inertia force is $ma$ downwards.

Motion

Motion equations

The following are the equations of motion:

Average velocity: $v=\frac{ds_t}{dt}$
Average acceleration: $a=\frac{dv_t}{dt}$
$s=ut+\frac{1}{2}at^2$
$v=u+at$
$v^2=u^2+2as$
$s=\frac{(v+u)t}{2}$

Where $v$ is the final velocity, $u$ is the initial velocity, $a$ is the acceleration, $t$ is the time, and $s$ is the displacement.

Circular motion

The following are the equations of motion for circular motion:

$\omega = \frac{\Delta\theta}{\Delta t}=\frac{2\pi r}{t} = \frac{v_t}{r}$
$v_t = r\omega$
$a_c = r\omega^2 = \frac{v_t^2}{r}$
$a_t = r a_c$
$F_c = \frac{mv_t^2}{r} = ma_c$
Total acceleration: $a_{to} = \sqrt{a_t^2+a_c^2}$
Accelerating cylinder/disk: $F = \frac12mra,\ Fr=Ia_c$

$I_{disk}=\frac12mr^2$

$\omega$ is the angular velocity, which describes change in angle over time\ $\{v_t,\ a_t\}$ is the tangential velocity and acceleration, which is tangential to any point on the radius\ $\{a_c,\ F_c\}$ is the centripetal acceleration and force, which are perpendicular to tangential quantities. They act on the object, hence they be seen as normal forces.\ $a_{to}$ is the total acceleration, which is the resultant of $a_t$ and $a_c$

Direction of angular velocity

The direction of the angular velocity is given by the right-hand rule. If the fingers of the right hand curl in the direction of rotation, the thumb points in the direction of the angular velocity.

Instantaneous center of zero velocity

The instantaneous center of zero velocity is the point on a rotating object that has zero velocity. The velocity is perpendicular to the radius (edge) at that point.

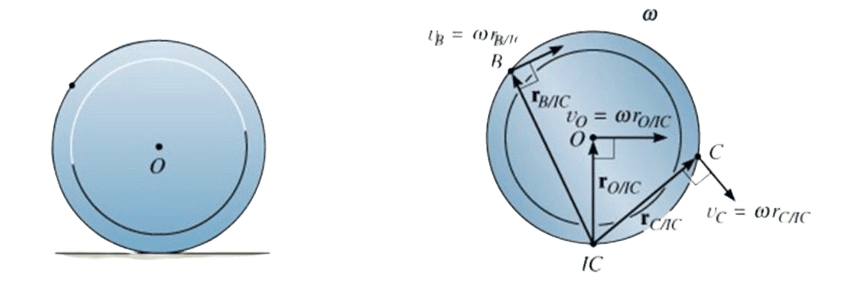
The velocity at any point is given by:

v=\omega d

Where $d$ is the distance from the IC.

Momentum and impulse

Momentum and conservation of momentum

Momentum is the product of an object's mass and velocity. It is a vector quantity.

p=mv

The principle of conservation of momentum states that the total momentum of a system remains constant if no external forces act on it.

F_{ext}=0\ ?\ p=\text{const}

The angular momentum about a point $O$ is given by:

H_O=Iw=mv_i\times r

Coefficient of restitution

The coefficient of restitution is a measure of how much kinetic energy is conserved in a collision. It is given by:

e=|\frac{v_{2}-v_{1}}{u_{1}-u_{2}}|

Where $v_{1}$ and $v_{2}$ are the final velocities, and $u_{1}$ and $u_{2}$ are the initial velocities.

$e=1$ is a perfectly elastic collision
$e=0$ is a perfectly inelastic collision
$0<e<1$ is a (partially) elastic collision

Impulse (impact)

Impulse is the change in momentum of an object. It is given by:

\Delta p=F\Delta t

Vibrations

Simple harmonic motion

Simple Harmonic Motion equations

The following are the equations of motion for simple harmonic motion:

$x=A\sin(wt+\phi)$
$f=\frac{1}{T}=\frac{w}{2\pi}$
$T_{vertical} = 2\pi\sqrt{\frac{m}{k}}$
$T_{swing} = 2\pi\sqrt{\frac{l}{g}}$ Where $A$ is the amplitude. $\phi$ represents the angle of which the motion starts. ( $\Delta\phi$ for $x$ from $x=0$ to $x:t=0$ )

Natural frequency

The natural frequency of a spring mass system is the frequency at which the system oscillates when displaced from equilibrium.

w_0=\sqrt{\frac{k}{m}}

Where $f$ is the frequency, $k$ is the spring constant, and $m$ is the mass.

Spring mass system

Hooke's law

Hooke's law states that the force required to extend or compress a spring is directly proportional to the extension or compression.

F=-kx

Where $F$ is the force, $k$ is the spring constant, and $x$ is the extension or compression.

Damping & damping coefficient

Damping is the process of reducing the amplitude of an oscillation. It is given by:

F_d=-cv

Where $F_d$ is the damping force, $c$ is the damping coefficient, and $v$ is the velocity.

Critical damping

Critical damping is the minimum amount of damping required to prevent oscillation. It is given by:

c_{crit}=2\sqrt{mk}

The following gives the cases of damping:

Underdamping: $c<c_{crit}$
Overdamping: $c>c_{crit}$
Critical damping: $c=c_{crit}$ Critical damping gives the fastest return to equilibrium.

Energy, work and power

Work

Work done is the energy required to move an object. It is given by:

W=Fd

Energy

The following are the types of energy:

Kinetic: $E_k=\frac{1}{2}mv^2$
Gravitational potential: $E_{GP}=mgh$
Elastic potential: $E_{EP}=\frac{1}{2}kx^2$
Friction: $E_{f}=F_f\times d=\mu Nd$
Rotational: $E_{r}=\frac{1}{2}Iw^2=\frac14mv_t^2$

The energy of a spring-mass system is given by:

E=E_k+E_{EP}

Conversation of energy

The principle of conservation of energy states that the total energy of a system remains constant if no external forces act on it.

F_{ext}=0\ ?\ E=\text{const}

This means in a system, energy is converted from one form to another. Use this fact to solve for unknowns.

Power

Power is the rate at which work is done. It is given by:

P=\frac{W}{t}

Power and acceleration

The power required to accelerate an object is given by:

P=Fv

Where $F$ is the force, and $v$ is the velocity.

Dynamics