NotesAtHKU

Axial loading refers to the application of a force along the axis of the member.

Stress and strain

Axial stress

Axial stress is the stress that is parallel to the cross-sectional area of the member. It is given by:

\sigma=\frac{F}{A} (Nm^{-2})

Where $F$ is the force applied, and $A$ is the cross-sectional area of the member. Note that $1 Pa = 1 Nm^{-2}$ .

Eccentric loading and stress

When a force is applied off-centre to the member, the stress at each end is given by:

\sigma=\frac{\sum F}{wd}\pm \frac{6F\times e}{d\times w^2}

Where $w$ is the width of the member, $d$ is the depth of the member, and $e$ is the eccentric distance from the centroid of the member to the point of application of the force.

The $\pm$ sign is used to denote the maximum and minimum stress on opposite sides.

Axial strain

Axial strain is the ratio of the change in length to the original length of the member. It is given by:

\epsilon=\frac{\Delta x}{x} \text{(Ratio)}

Where $\Delta x$ is the change in length, and $L$ is the original length of the member.

Materials

Strength

Material strength is defined as the maximum stress that can be resisted by the material.

Young's Modulus

Young's modulus is the ratio of stress to strain, given by:

E=\frac{\sigma}{\epsilon}=\frac{Fx}{A\Delta x} (Pa, Nm^{-2})

Poisson's ratio

Poisson's ratio is the ratio of lateral strain $\epsilon_l$ to axial strain $\epsilon$ , given by:

\nu=-\frac{\epsilon_l}{\epsilon} (\text{Ratio})

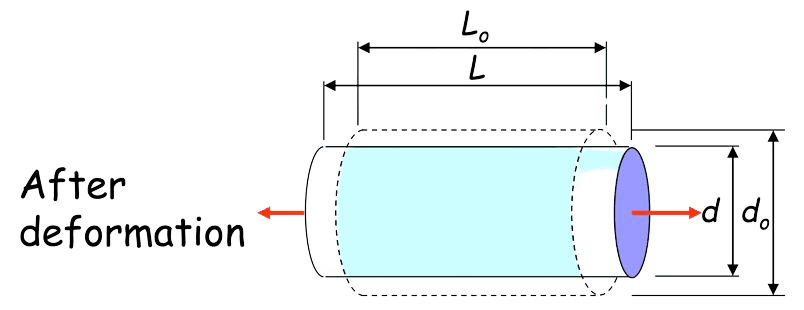
The lateral strain $\epsilon_l$ is $\frac{\Delta d}{d_0}$ .

Hydrostatic pressure

Hydrostatic/water pressure

The water pressure acting on any surface is always perpendicular to the surface, and the pressure is given by:

p=\rho gh (Pa, Nm^{-2})

Where $\rho$ is the density of water, and $h$ is the depth of the water.

Hence, we can see that the water pressure increases linearly with depth.

Water pressure load on slanted surface

The load exerted on a slanted surface by water pressure F is given by and located at:

F=\frac{\rho g d w L}{2} @ \frac{1}{3}L\ /\ \frac{2}{3}d

Where $d$ is the depth of water, $w$ is the width of the volume, and $L$ is the length of the surface.

Internal tensile stress

Internal tensile stress (hoop stress) refers to the stress caused by the internal force, acting along the circumferential direction of a cross section.

\sigma_{\text{pipe}}=\frac{Pd}{2t}, \sigma_{\text{sphere}}=\frac{Pr}{2t}

Where $P$ is the internal pressure, and $t$ is the thickness.

Axially loaded members