Notes@HKU by Jax

Bending forces and stress

Internal force in beams

When we consider the internal forces of a beam, we take a cross section and consider the forces acting on it. The internal forces are:

  • Shear force VV is the force acting parallel to the cross-section.
  • Bending moment MM is the moment generated by the variation of forces acting perpendicularly to the cross-section.

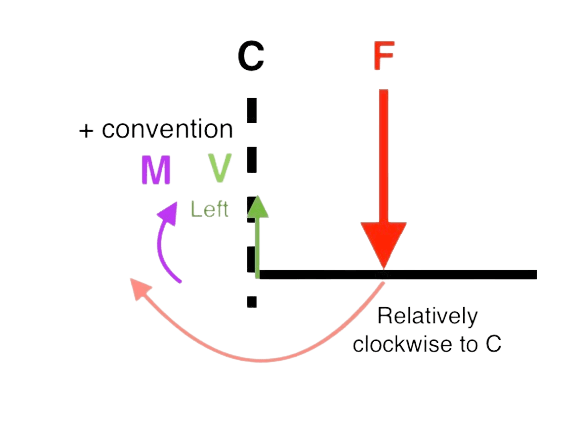
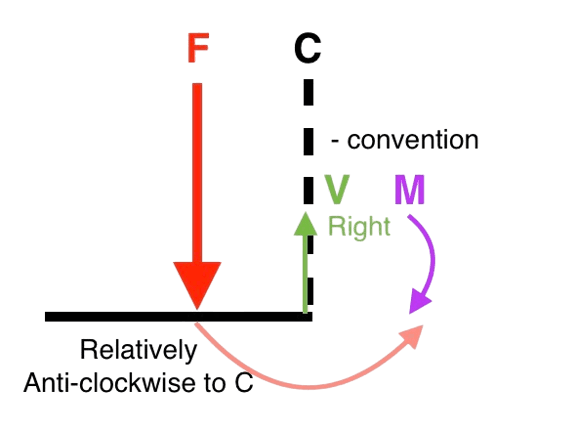
Sign convention of internal forces

{+↻}\{+\circlearrowright\} The idea is that if the acting force is relatively clockwise to the cross-section CC, it is positive. The following is the signs of internal forces for a positive moment:

  • V: ↻\circlearrowright (L ↑\uparrow R ↓\downarrow)
  • M: ↷↶\curvearrowright\curvearrowleft (sagging moment is positive)

Couple moments

When considering couple moments, their effect is independent of the point of application, but they have no effect if they are not in the cut of the beam during analysis. They do not exert any force on the beam, but will affect the reaction forces at supports.

Finding internal forces by side

To find the internal forces at cross-section CC where no loads apply, we consider the left and right side of the section:

  • V: ∑F\sum F on either side
  • M: ∑MC\sum M_C on either side about CC

Note that the sums are all signed by convention. (e.g. A force FF is positive if it points upwards on the left side.)

This also gives us the fact that ∑FL=∑FR\sum F_L =\sum F_R and ∑ML=∑MR\sum M_L =\sum M_R, signed by convention on both sides.

Finding interal forces on left and right sides

To find the interal forces at the left and right cross-section at a point CC where loads or moments apply:

  1. Left side: {↑R====↓V↺M… }\{\overset{R}{\uparrow}====\overset{V}{\downarrow}\overset{M}{\circlearrowleft}\dots\}
  2. Right side: {…↑V↻M====↑R}\{\dots\overset{V}{\uparrow}\overset{M}{\circlearrowright}====\overset{R}{\uparrow}\}

Diagramming internal forces

Diagramming internal forces

The two internal force diagrams are V(x)−xV(x)-x and M(x)−xM(x)-x diagrams. V(x)V(x) gives the shear force VV at distance xx from the left side of the beam.

Relation between internal forces

The following is the relation between the internal forces:

dMdx=VdVdx=−w\frac{dM}{dx}=V \frac{dV}{dx}=-w

Where ww is the distributed load acting on the beam.

  • This tells us that the slope of the M(x)M(x) diagram at an interval is the value of VV at that interval.
  • This tells us that the slope of the V(x)V(x) diagram at an interval is the value of −w-w at that interval.

Steps to follow

  1. Solve for reaction forces
  2. Draw the FBD of a cut from the leftmost side to a location with distance xx from the leftmost force not analysed
  3. Analyse the FBD of the cut (solve for VV and MM)
  4. Draw the graphs in the cuts and repeat for all cuts

Figurative steps:

  1. →RA,RB...\to R_A, R_B...
  2. {↑R =====⏟x ↓V↺M… }\{\overset{R}{\uparrow}\ \underbrace{=====}_x\ \overset{V}{\downarrow}\overset{M}{\circlearrowleft}\dots\}
  3. →V,M\to V, M
  4. →V(x),M(x)\to V(x), M(x)

To analyse a distributed load ww, consider the FBD of the whole system on the left, then let xx be the distance from the leftmost force analysed:

\large

{=↑R==2=↓F====↓w⋅x⏟x↓V↺M… }\{\underset{\underset{R}{\uparrow}}{=}\underset{2}{==}\overset{\overset{F}{\downarrow}}{=}\underbrace{\overset{\overset{w\cdot x}{\downarrow}}{====}}_x\overset{V}{\downarrow}\overset{M}{\circlearrowleft}\dots\}

Signing conventions

By convention, we consider the positive convention with respect to the cross-section. That means, if the force is clockwise to the cross-section, it is positive..

Bending stress

Pure bending

A section of the beam is said to be under pure bending if:

V=0,M constantV=0, M\text{ constant}

Netural axis

The neutral axis always passes through the centroid of the beam. It is netural as the length remains unchanged for the surface that the axis passes through.

The distance from the netural axis is denoted yy (positive downwards).

Section modulus

The section modulus is given by:

Z=Wz=IyZ=W_z=\frac{I}{y}

Bending stress

The bending stress σ\sigma is given by:

σ=MyI\sigma=\frac{My}{I}

Where MM is the bending moment, yy is the distance from the neutral axis (centroid), and II is the moment of inertia of the section.

The formula also tells us that the bending stress is proportional to the distance from the neutral axis, and the neutral axis experiences no stress.

Related: Moment of inertia

Maximum tensile and compressive stress

σmax↕=My↕I\sigma^\updownarrow_{max}=\frac{My_\updownarrow}{I}

The maximum tensile and compressive stress σmax\sigma_{max} at a cross section is located at the top σ↑\sigma^\uparrow and bottom edge σ↓\sigma^\downarrow. Note that tensile stress is positive (unlike tension which is negative).

Edit on GitHub

Previous

Centroids and moment of inertia

Next

Dynamics

On this page