Polar Coordinates & Hyperbolic Functions
Polar Coordinates
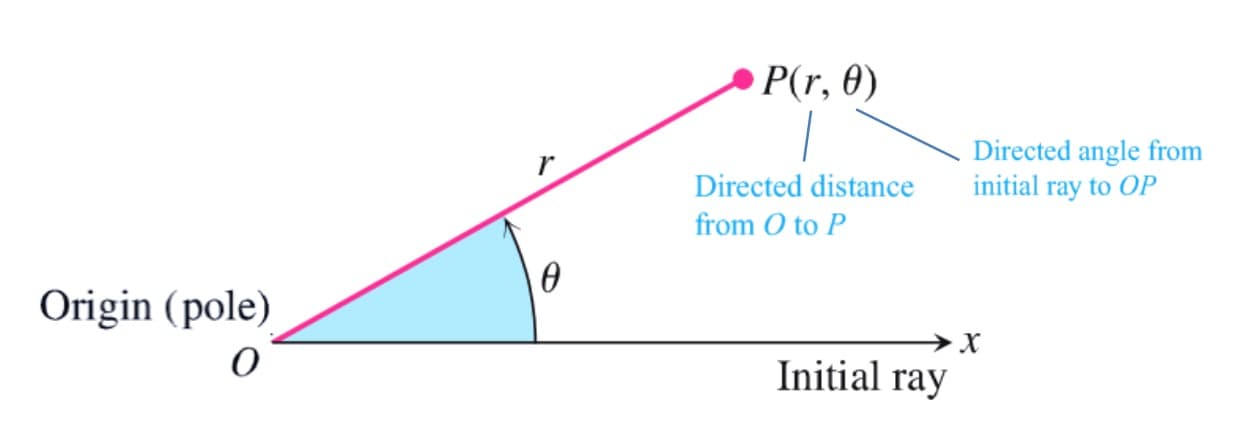
We can convert a Cartesian equation to polar equation using:
We can also see that:
The polar equation for the circle is simply .
We can easily graph any polar formula following the following steps:
- Plot graph. If the function involves trigo functions, we can simply translate its graph. The height at a certain point is the distance from the origin.
- Then we can simply trace the graph from the left, and plot the points according to the distance from the origin at each angle. Using the eqations above, we can also find the Cartesian coordinates.
- If the graph is symmetric, we can simply copy the other half.