NotesAtHKU

Introduction to the concept of limit

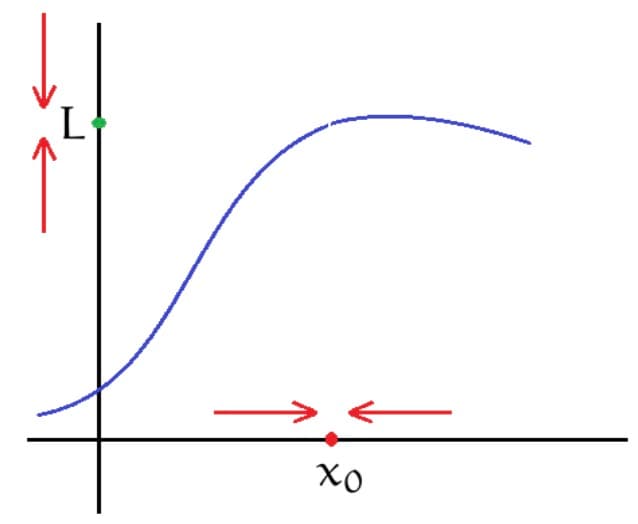
We can conceptualize that the limit of a function $f(x)$ is $L$ as $x$ approaches $c$ , given that we can make $f(x)$ as close to $L$ as we want for all $x$ sufficiently close to $a$ , from both sides, without actually letting $x$ be $a$ . We can write this as:

\lim_{x\to a}f(x)=L

One-sided limits

There are two sides that $x$ can tend to a number. We can write it as $x\to n^-$ and $x\to n^+$ , which represents from the negative (left) / positive (right) side.

Existence of limits

Condition for limit to exist

The limit for a function $f(x)$ only exists if and only if:

\lim_{x\to a^+}f(x)=\lim_{x\to a^-}f(x)

WARNING: If the limit is $\mathbf{\infty}$ it doesn't exist.

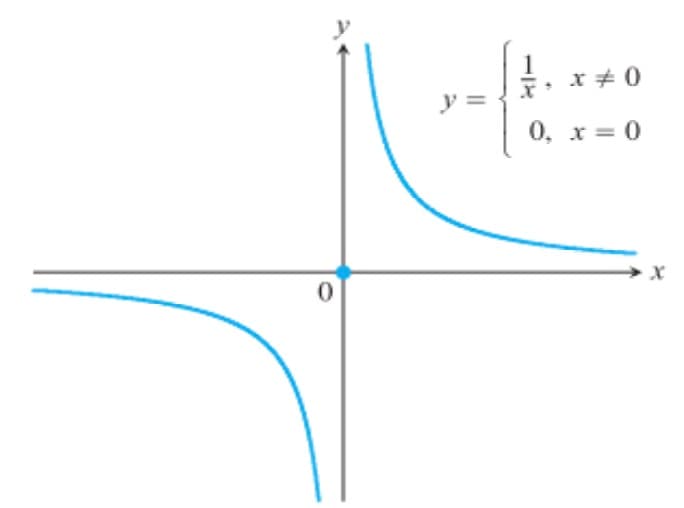
For this example, when $x\to 0^-, y\to -\infty$ .

Similarly, as $x\to 0^+, y\to +\infty$ .

Hence, we can conclude that the limit for this function as $x\to 0$ doesn't exist.

Continuity

A function $f(x)$ is continuous at $x=a$ if:

\mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left( a \right)

Continuity properties

For $f,g$ continuous at $c$ , the following are also continuous at $c$ :

$f \pm g$
$kf$
$fg$
$\frac{f}{g}$ , given that $g(c)\ne 0$

Intermediate value theorem (IVT)

If a function $f$ is continuous on $[a, b]$ , there is a number $c$ in $[a, b]$ where $f(c)$ in $[f(a), f(b)]$ .

We use the IVT by first finding $f(a)$ and $f(b)$ , then apply the rule.

To prove that there is a root, we can use the IVT by showing there is a change of sign between the interval given.

Computing limits

Indeterminate forms

Indeterminate forms are forms that cannot be solved by simply substituting the value of $x$ into the function. They are:

\frac{0}{0}, \frac{\infty}{\infty}, 0\cdot\infty, \infty-\infty, \infty^0, 1^\infty, \infty^0

Note that $\infty + \infty = \infty$ . Related: L'Hopital's rule

Using the limit laws

For functions $f,g$ and using $\mathop {\lim }\limits_{x \to a}=\bigcirc$ for simpler notation:

$lim_{x\to a}c=c$
$\bigcirc(f\pm g)=\bigcirc f\pm \bigcirc g$
$\bigcirc(k\cdot f)=\bigcirc k\cdot\bigcirc f$
$\bigcirc(f^n)=(\bigcirc f)^n$
$\bigcirc(fg)=\bigcirc f\bigcirc g$
$\bigcirc(\frac{f}{g})=\frac{\bigcirc f}{\bigcirc g}, \text{given that }\bigcirc g\ne 0$ . This strict condition prevents indeterminate forms. We can use these laws to break a limit into separate limits, and compute that way. Also note that:
$\bigcirc f(g)=f(\bigcirc g),$ given that $f$ is continuous at $\bigcirc g$

Limit of a polynomial

For the limit of a polynomial $p(x)$ :

lim_{x\to a}p(x)=p(a)

This can be proven easily with the limit laws above.

Techniques to compute limits

To solve for limits, we have to get the expression to the right form - a polynomial, for us to substitute our limit value into the function.

To do this, often we have to factorize or rationalize.

Limits of composite functions

For the limit of a composite function $\lim_{x\to a}f(g(x))$ , where $f$ is not continuous at $g(a)$ , we find $b$ as $x\to a,g\to b$ , and then find $\lim_{x\to b}f(x)$ at that value.

The following explains some common cases:

$x\to a^-, g\to g(a)^-$
$x\to a^-, -x\to -a^+$

For $y=\lim_{x\to a}f(x)^{g(x)}$ , we can the logarithm to simplify the function, and determine $\lim_{x\to a}\ln y$ and find $\lim_{x\to a}y=e^{\lim_{x\to a}\ln y}$ .

Limits of square roots

To solve for limits of square roots, we can multiply by the conjugate to rationalize the function.

\lim_{x\to a}f(x)+\sqrt{g(x)}=\lim_{x\to a}\frac{f^2(x)-g(x)}{f(x)-\sqrt{g(x)}}

The squeeze / sandwich theorem

Suppose $f(x)\le g(x) \le h(x)$ in the range $[a, b]$ , for $c$ in $[a, b]$ :

\lim_{x\to c}f \le \lim_{x\to c}g \le \lim_{x\to c}h

We will make use of the fact that the limits can be equal to solve for the limit of $g(x)$ .

When we can't seem to factorize a function, we can try squeezing it between two other functions.

\lim_{x\to 0}x^2\cos\frac{1}{x}

We know the limits of the function $\cos \frac{1}{x}$ , so we can start from there.

\text{Given that }x\ne 0, -1\le \cos \frac{1}{x} \le 1

\text{Multiplying }x^2\text{ on both sides},-x^2\le \cos x^2\frac{1}{x} \le x^2

\text{As }\lim_{x\to 0}\pm x^2=0, \text{we can conclude that }\lim_{x\to 0}x^2\cos\frac{1}{x}=0

Infinite limits

Determining infinite limits

If $f(x)$ gets (negatively) arbitrarily large when $x$ approaches $a$ , we can say:

\lim_{x\to a}f(x)=(-)\infty

After we know that the limit may be infinity, we then have to make sure that the limit is the same from both sides, so that the limit is actually $\infty$ . We can do so by plugging numbers which are approaching the limit from both sides.

Infinite limit exists

\lim_{x\to 0}\frac{6}{x^2}

\text{Consider both}\ \lim_{x\to 0^-}\frac{6}{x^2},\lim_{x\to 0^+}\frac{6}{x^2}:

\lim_{x\to 0}\frac{6}{x^2}=\infty

Infinite limit doesn't exist

\lim_{x\to 4}\frac{3}{(4-x)^3}

Checking both sides, we can conclude that the limit doesn't exist, as:

\lim_{x\to 4^+}\frac{3}{(4-x)^3}=-\infty, \lim_{x\to 4^-}\frac{3}{(4-x)^3}=\infty

Limits at infinity

Infinity operations

Note the following operations:

$\infty + k=\infty$
For $k<0,\ k\infty=-\infty$
$-\infty\times\infty=-\infty$

Determining limits of infinity

It is not hard to see that, for rational numbers $n$ :

\lim_{x\to\pm\infty}\frac{k}{x^n}=0

The easiest way to determine the limit would be to factorize the function so that we can use the fact above.

Determining limits of infinity of polynomials

Using the above fact, we can see that for a polynomial $p(x)$ with degree $n$ and largest coefficient $a_n$ :

\lim_{x\to\pm\infty}p(x)=a_nx^n

Which means we can only consider the largest term in a polynomial for limits of infinity.

Indeterminate forms by substitution of infinity

Substituting $\infty$ into the function gives $\infty-\infty-\infty$ , which is indeterminate. Hence, we must factorize it.

\begin{aligned}\lim_{x\to\infty}2x^4-x^2-8x & =\lim_{x\to\infty}[x^4(2-\frac{1}{x^2}-\frac{8}{x^3})] \\ & =\infty\times 2 \\ & =\infty \end{aligned}

Or we can just simply use the theorem above and consider $\lim_{x\to\infty}2x^4$ only to give $\infty$ .

Factor polynomials limit to infinity

We can simply cbonsider the largest terms on each side and give the final answer easily.

\begin{aligned} \lim_{x \to -\infty } \frac{{\sqrt {3{x^2} + 6} }}{{5 - 2x}} & =\lim_{x \to -\infty }\frac{\sqrt{3x^2}}{-2x} \\ & =\lim_{x \to -\infty }\frac{\sqrt{3}|x|}{-2x} \leftarrow \sqrt{x^2}=|x| \\ & =\lim_{x \to -\infty }\frac{-\sqrt{3}}{-2} \leftarrow |c|,c<0=-c \\ & =\frac{\sqrt{3}}{2} \end{aligned}

Note that, as we are considering the negative limit of infinity, we need to add - to the abs sign on line 3.

Asymptotes

Vertical asymptotes

$f$ will have v-asymptotes at $x=a$ if any $\pm$ is true:

\lim_{x\to a^\pm}f(x)=\pm\infty

Horizontal asymptotes

$f$ will have h-asymptotes at $y=L$ if any $\pm$ is true:

\lim_{x\to\pm\infty}f(x)=L

Related: Graphing functions

Limits and Continuity

Introduction to the concept of limit

One-sided limits

Existence of limits

Condition for limit to exist

Continuity

Continuity

Continuity properties

Intermediate value theorem (IVT)

Computing limits

Indeterminate forms

Using the limit laws

Limit of a polynomial

Techniques to compute limits

Limits of composite functions

Limits of square roots

The squeeze / sandwich theorem

Infinite limits

Determining infinite limits

Infinite limit exists

Infinite limit doesn't exist

Limits at infinity

Infinity operations

Determining limits of infinity

Determining limits of infinity of polynomials

Indeterminate forms by substitution of infinity

Factor polynomials limit to infinity

Asymptotes

Vertical asymptotes

Horizontal asymptotes

On this page