NotesAtHKU

First principle

The first principle is the definition of the derivative of a function $f(x)$ at $x=a$ :

f'(x) = \frac{d}{dx} f(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}

Note the notation of prime ( $'$ ), which denotes the derivative against $x$ for any function primed.

Differentiability

The function is differentiable at $x=a$ if:

\lim_{x\to a^-}f'=\lim_{x\to a^+}f'

Use first principle if the function is cased.

Differentiation formulas and rules

Basic formulas

We can differentiate individual items: $\displaystyle {\left( {f \pm g} \right)^\prime } = f' \pm g'$
We can factor out a multiplicative constant: $\displaystyle {\left( {cf} \right)^\prime } = cf'$
Derivative of a constant is 0: $\frac{d}{dx}k = 0$
Power rule: $\frac{d}{dx}x^n = nx^{n-1}$

Chain rule

Shorthand: d1x2 + d2x1

(u(v))'=u'(v)v'\quad\quad\text{or}\quad\quad\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}

Product rule

Shorthand: d from outside to inside

(uv)' = uv' + vu'\quad\quad\text{or}\quad\quad\frac{d}{dx}(uv)=u\frac{dv}{dx}+v\frac{du}{dx}

Quotient rule

Shorthand: move lower d upper - d lower x upper, lower square

(\frac{u}{v})'=\frac{vu'-uv'}{v^2}\quad\quad\text{or}\quad\quad\frac{d}{dx}(\frac{u}{v})=\frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2}

	$f(x)$	$f'(x)$
1.	$a^x$	$\ln{a}\cdot a^x$
2.	$e^{kx}$	$ke^{kx}$
3.	$\ln{kx}$	$x^{-1}$
4.	$\\|x\\|$	$\frac{\\|x\\|}{x}$
5.	$\sin kx$	$k\cos kx$
6.	$\cos kx$	$-k\sin kx$
7.	$\tan kx$	$k\sec^2 kx$
8.	$\csc x$	$-\csc x \cot x$
9.	$\sec x$	$\sec x \tan x$
10.	$\cot x$	$-\csc^2x$
11.	$\sin^{-1} x$	$(\sqrt{1-x^2})^{-1}$
12.	$\cos^{-1} x$	$-(\sqrt{1-x^2})^{-1}$
13.	$\tan^{-1} x$	$(1+x^2)^{-1}$

Techniques of differentiation

Parametric differentiation

For a parametric equation $y=f(t)$ and $x=g(t)$ :

\frac{dy}{dx}=\frac{dy}{dt}\div \frac{dx}{dt}

Inverse functions

$f^{-1}(x): f(x)\leftrightarrow x$ (switch $x$ and $y$ ).

Inverse functions only exists in the domain of $f$ where $f$ is bijective (one-to-one and onto). This means that the domain where $f$ gives unique values is the range of $f^{-1}$ .
The range of $f$ is the domain of $f^{-1}$ .
The domain of $f$ is the range of $f^{-1}$ .

Derivative of Inverse functions

At $c$ , we first find $f'(x)$ and the value of $f^{-1}(c)$ , then we apply the formula to find the value of $f^{-1'}(c)$ :

f^{-1'}(c)=\frac{1}{f'(f^{-1}(c))}

$f^{-1}(c)$ can be found by solving $f(x)=c$ .

Implicit differentiation

Differentiate all $xy$ , add $y'$ behind all differentiations of $y$ .

To find $y'$ for $y^2=x^2+\sin(xy)$ :

\begin{aligned} y^2 & =x^2+\sin(xy) \\ 2yy' & =\frac{d}{dx}(\sin(xy)) \\ 2yy' & =2x+\cos(xy)(xy'+y) \\ \text{Then we simply collect terms of } & y' \\ y' & =\frac{2x+y\cos(xy)}{2y-x\cos(xy)} \end{aligned}

To find the second derivative $y''$ , differentate the expression and substitute $y'$ back in.

Logarithmic differentiation

To differentiate a function to the power of another function, we can take the logarithm of the function, then differentiate.

\begin{aligned} (f^g)' & =(e^{g\ln f}) \\ & = (g\ln f)'e^{g\ln f} \end{aligned}

To find $\frac{dy}{dx}$ for $y=x^x$ :

\begin{aligned} y & = e^{x\ln x} \\ & = e^{x\ln x}(\ln x+x\frac{1}{x}) \\ & = x^x(\ln x+1) \end{aligned}

L'Hopital's rule

For any $a\in [\mathbb{R}, \pm\infty]$ , if $\lim_{x\to a}(\frac{f}{g})$ is in indeterminate form after substitution, we can conclude:

\lim_{x\to a}(\frac{f}{g})=\lim_{x\to a}(\frac{f'}{g'})

To find $\lim_{x\to-\infty}xe^x$ , we first check if the limit is indeterminate, then we can apply the rule:

\begin{aligned} \lim_{x\to-\infty}xe^x & \implies \infty\times0 \\ \lim_{x\to-\infty}xe^x & = \lim_{x\to-\infty}\frac{x}{e^{-x}} \\ & = \lim_{x\to-\infty}\frac{1}{-e^{-x}}\text{ (rule applied)} \\ & = 0 \end{aligned}

Important theorems

Mean value theorem (MVT)

For $f(x)$ that is continuous in $[a,b]$ and differentiable in $(a,b)$ :

f'(c)=\frac{f(b)-f(a)}{b-a},\quad c\in(a,b)

The theorem tells us that, in described conditions, there must be a point $c$ where the slope of the tangent line is equal to the slope of the line from $a\to b$ (secant line).

Rolle's theorem

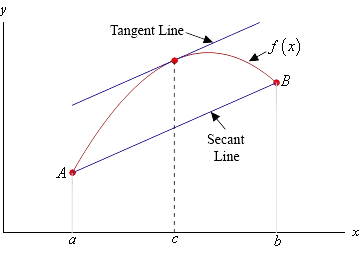
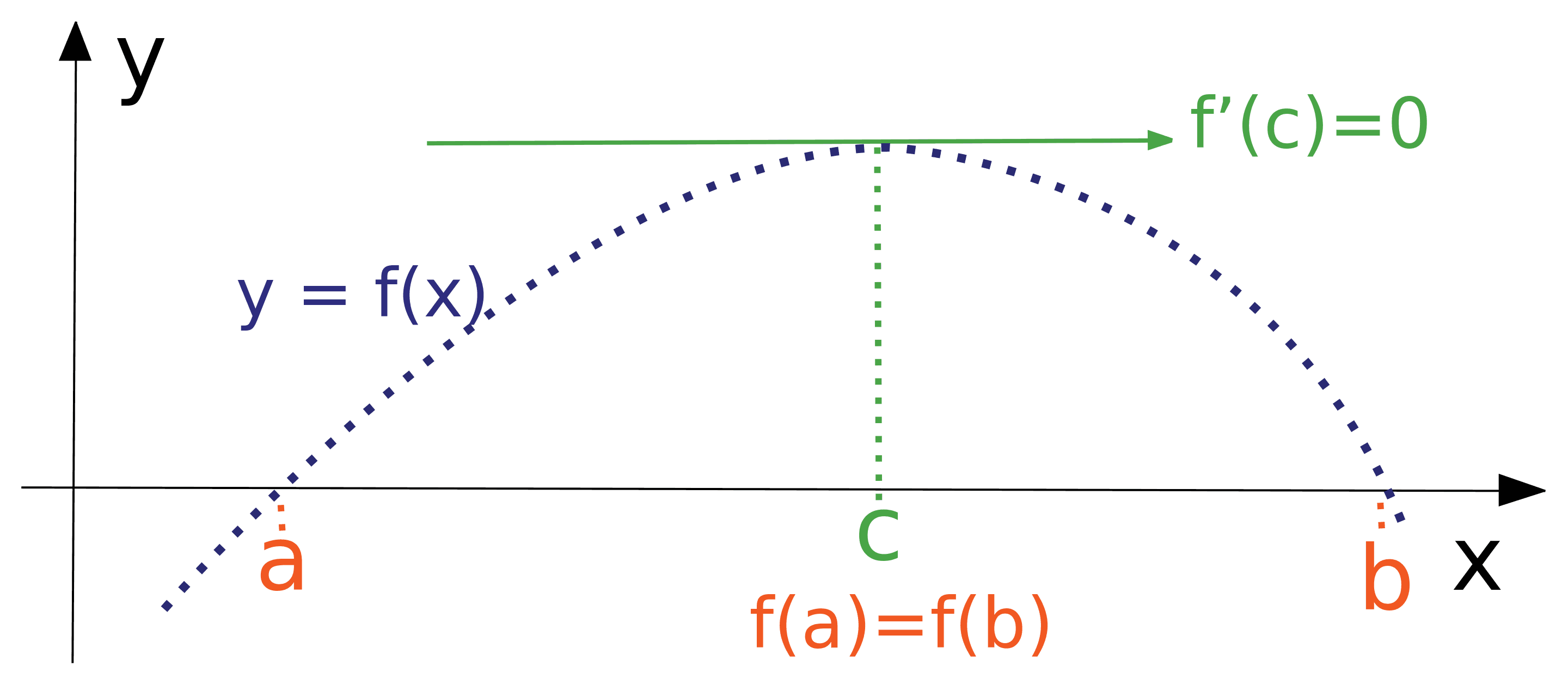
For $f(x)$ that is continuous in $[a,b]$ and differentiable in $(a,b)$ :

\forall\ f(a)=f(b)\text{ there exists }f'(c)=0,\quad c\in(a,b)

For $F'=f$ , if $F$ has 4 roots, then $f$ has 3 roots.

Extremum points

Critical and inflection points

A critical point is a point where $f'(x)=0$ or undefined, or the end-points of the domain if inclusive.

An inflection point is a point where $f''(x)=0$ or undefined, that the concavity of the function changes.

Max/minimum points

The absolute maximum/minimum points are the points where the function has the largest/smallest value in the entire domain.

The local maximum/minimum points are the points where the function has the largest/smallest value in a small interval around the point.

Determining shape of graph

Concavity

Concavity is the direction of the curve, and can be described by the values of $f'$ and $f''$ :

$f''$	$-$	$+$	$+$	$-$
$f'$	$-$	$+$	$-$	$+$
$f$

Note: Arrows goes clock-wise.

	Step	Expression
1.	Determine domain of function
2.	Special points without continuity?
3.	Axis intercepts	$(f(x)=0, 0)\ (0, f(0))$
4.	Critical points	$f'(x)=0$ or undefined
5.	Point maxima?	$+f''(x)$ or $-f''(x)$
6.	Inflection points	$f''(x)=0$ or undefined
7.	Horizontal asymptotes	$\lim_{x\to\pm\infty}f(x)=n?$
8.	Vertical asymptotes	$\lim_{x\to a^\pm}f(x)=\pm\infty?$
9.	Area strictly increasing/decreasing?	$f'(x)>0$ or $f'(x)<0$
10.	Area concavity?	$-++-/-+-+/$

Related: Definition of asymptotes

Higher derivatives

Derivatives of higher order (e.g. $f''(x), f'''(x)$ ) can be expressed as $f^{(n)}(x)$

Derivatives